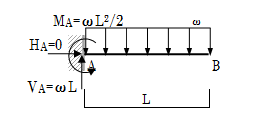
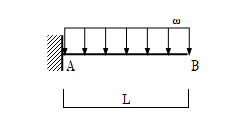
次に片持ち梁の支点反力計算を解説していきます。図1-2-9に示すように、A点を固定端とした片持ち梁に等分布荷重ωが作用した時の支点反力を求めていきます。
単純梁の時と同様に、まずは支点反力の設定を行います。図1-2-10に示すようにA点の鉛直方向支点反力をVA、水平方向支点反力をHA、モーメント反力をMAとします。固定端なので、モーメント反力もありますので忘れないようにしてくださいね。
支点反力の荷重の向きは、先ほどと同じように正の向きで設定します。
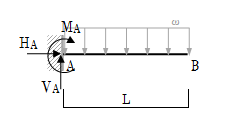
まずは、X方向(水平方向)について解いていきます。X方向については、HA以外に水平方向の力は無いので、HAの反力は0となります。
∑X=HA=0 (式1.3.10)
∴HA=0 (式1.3.11)
次に、Y方向(鉛直方向)について解いていきます。鉛直方向の力としては、等分布荷重ωと支点反力VAがあります。
分布荷重が作用している場合、まず分布荷重の合力を求めます。分布荷重の合力は、荷重の大きさを図形としてみたときの面積となります。今回の問題の等分布荷重ωは、単位長さ当たりの荷重なので「等分布荷重ωに等分布荷重が作用している長さLを掛けた合力ωL」が、重心位置に作用していると考えます。
∑Y= VA-ωL=0 (式1.3.12)
∴VA=ωL (式1.3.13)
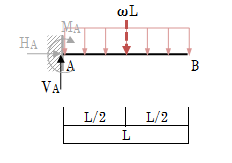
A点にはモーメント反力が発生することから、モーメントによる釣り合いを考える必要があります。A点によるモーメントの釣り合いについて考えれば、HA及びVAについては距離0となることから、MAと等分布荷重の合力ωLによるモーメントの釣り合い式をたてることができます。
∑M=MA+ωL×L/2=0 (式1.3.14)
∴MA=-(ωL^2)/2(反時計回り) (式1.3.15)
MAは時計回りとして設定していましたが、計算結果で負の値となりましたので、反時計回りでωL2/2のモーメントが正解となります。
以上の計算結果より、支点反力は図1-2-13の通りとなります。