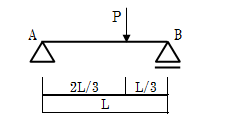
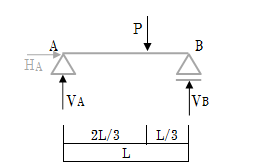
ここからは実際に支点の反力計算を行っていきます。まずは、単純梁の支点反力計算について解説していきます。図1-2-3に示すようにA点がピン支持、B点がローラー支持、長さLの梁にA点から2L/3の位置に集中荷重Pが作用した時の支点反力計算を求めていきます。
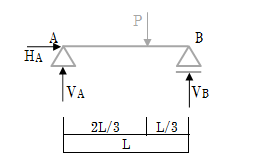
まず、支点反力を求めるためには、支点反力の向きを想定します。A点はピン支持なので、「水平反力」と「鉛直反力」が支点反力として発生します。ここでは、A点の水平反力を「HA」、鉛直反力を「VA」と設定します。一方、B点はローラー支持なので、「鉛直反力」が支点反力として発生します。同じように、B点の鉛直反力を「VB」と設定します。
また、A点及びB点の支点反力の向きは図1-2-4のように想定します。ある程度、力学が得意な人であれば荷重に対して反力の向きが想定できるのですが、想定できない場合はまずは荷重の「正」の向きに反力を想定します。図1-2-5に示すように、一般的に、水平荷重では右向き、鉛直荷重では上向き、モーメント荷重では時計回りを正の向きとします。
軸方向の呼び方は、一般的に水平方向をX方向、鉛直方向をY方向と呼びます。
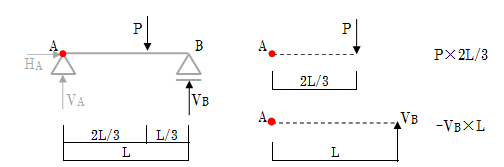
実際に力の釣り合いによる計算をしていきます。力の釣り合いでは、各方向の力の合計が0となります。
まずは、X方向(水平方向)について解いていきます。X方向については、HA以外に水平方向の力は無いので、HAの反力は0となります。
∑X= HA=0 (式1.3.1)
∴HA=0 (式1.3.2)
次にA点周りの曲げモーメントの釣り合い式について解いていきます。なぜA点周りの曲げモーメントの釣り合い式なのかというと、VAの作用線はA点を通っているのでVAによるモーメントは0となり、VAについて考えなくてよいからです。よって、
∑MA= P×2/3 L-VB×L=0 (式1.3.3)
∴VB=2/3 P(↑) (式1.3.4)
となり、VBの支点反力を求めることができます。
次に、Y方向(鉛直方向)について解いていきます。式を立てると、
∑X= VA+VB-P=0 (式1.3.5)
となります。支点反力VA及びVBは上向きなので正の値、集中荷重Pは下向きなので負の値となります。(式1.3.5)に(式1.3.4)を代入すると、VAの反力を求めることができます。
VA+2/3P-P=0 (式1.3.6)
∴VA=P/3(↑) (式1.3.7)
ちなみに、④でX方向(水平方向)力の釣り合いによりVAの支点反力を求めましたが、B点周りのモーメントの釣り合い式からも求めることができます。
∑MB=VA×L-P×L/3=0 (式1.3.8)
∴VA=P/3(↑) (式1.3.9)