たわみの公式が覚えられない人向けに、モールの定理によるたわみの公式の導き方を解説していきます。
私個人的には語呂合わせとかで覚えるのが苦手だったので、試験で忘れたときにこの方法でたわみの公式を求めていましたが、覚えられる人は語呂合わせで覚えて頂いた方がいいです。
(人見知りマンさんが先日、語呂合わせ暗記法を公開してますので参考までに…↓↓)
【一級建築士学科試験対策】たわみの公式一気に覚える語呂合わせ暗記法!【構造力学】力学が苦手な人必見!!
モールの定理とは…
モールの定理では、単純梁や片持ち梁に集中荷重や等分布荷重が作用した時のたわみや回転角を求めることができます。ここでは、求め方の計算手順を紹介します。
なんでそんな計算をするの?って思う人は次回以降にまた解説しますのでそちらを見てください。(恐らく、一級建築士受験生向けというよりは、構造力学を学ぶ大学生向けの内容となると思いますので、基本的には見なくていいと思います…確か、微分方程式とか使ったような…)
モールの定理による計算手順(集中荷重)
<単純梁の場合>
ピン接合とローラー接合で支持された梁(長さL)に集中荷重Pが梁の中央に作用した場合のたわみの公式を求めていきます。

①集中荷重Pが作用した時のモーメント図を求めます。

② ①で求めたモーメントに(-1/EI)を掛けた値を荷重(三角形分布の等分布荷重)として考えます。
-1/EIを掛けるというのは分かりにくいと思うので、「モーメントMをEIで割って、上下反転させた荷重図(M/EI)を荷重として考える」と思ってください。
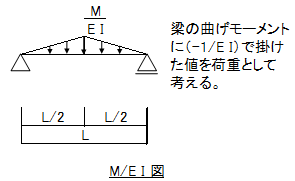
③ ②で求めた荷重に対して、反力及び梁中央の曲げモーメントを算出します。

この時の、梁中央の曲げモーメントMcの値が、梁のたわみとなります。(ちゃんとたわみの公式と同じでしょ!!)
すなわち、荷重が作用した場合のたわみを求めるには、曲げモーメントMにEIで割ったものを荷重(仮想荷重)とし、そのときの曲げモーメントの値が梁のたわみとなります。
ちなみに、M/EIの荷重におけるピン支点(左側の支点)の反力R=PL2/16EIは、回転角θを表しています。(θ=PL2/16EI)
(正確には、M/EIの荷重におけるせん断力⇒回転角を示します。)
<片持ち梁の場合>
片持ち梁(長さL)の先端に集中荷重Pが作用した場合のたわみの公式を求めていきます。
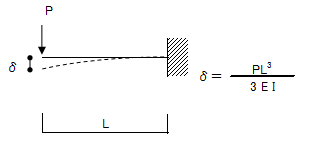
①集中荷重Pが先端に作用した時のモーメント図を求めます。
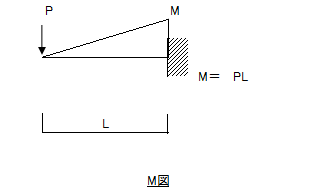
② ①で求めたモーメントに(-1/EI)を掛けた値を荷重(三角形分布の等分布荷重)として考えます。
この際、片持ち梁の場合のみ、固定端を自由端、自由端を固定端へ変更します。(固定端と自由端を入れ替えると覚えて頂いても大丈夫です。)
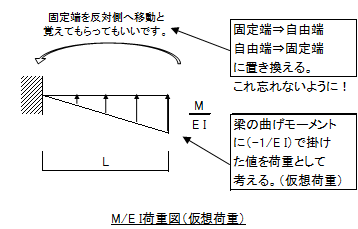
③ ②で求めた荷重に対して、反力及び梁中央の曲げモーメントを算出します。
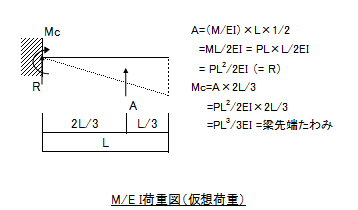
片持ち梁の場合でも同様に、自由端(左側)反力R=PL2/2EIは回転角θを表しています。(θ=PL2/2EI)
(正確には、M/EIの荷重におけるせん断力⇒回転角を示します。)
まとめると…
モールの定理によるたわみの公式の計算方法は、
① 曲げモーメント図(M図)を求める。
② ①で求めた曲げモーメントに(-1/EI)を掛けた値(M/EI図)を荷重(仮想荷重)として反力を求める。
②-2 片持ち梁の場合は、固定端と自由端を入れ替える。
③ ②の荷重によって求めた曲げモーメント⇒たわみ、せん断力⇒回転角を示します。
となります。