構造力学を学ぶ上での基本となる「静定力学」について解説していきます。「静定力学」では、力の釣り合い式で支点の反力や部材の応力を求めることができることができます。まずは、力学を計算する上で必要な知識となる「力の釣り合い」「支点のモデル化」について解説し、その後に支点反力や部材の応力計算について解説していきます。
ここでは、まず力の釣り合いについて解説していきます。
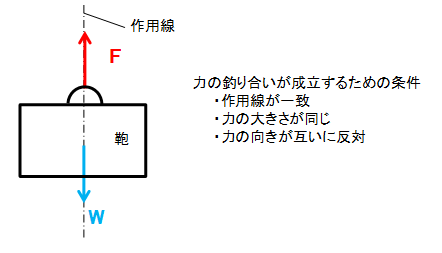
鞄を手で持ちあげると腕に力がかかりずっと持っていると疲れてきますよね。鞄には重力が作用しているので、下向きに力が作用しています。それに対して、鞄を持ち上げる力は反対に上向きとなります。鞄の重力による力をW、鞄を持ち上げる力をFとすると、図1-1-1のように表すことができます。
鞄を持っている状態では、当たり前ですが鞄は静止したままです。この鞄が動かない条件として、「2つの力の作用線が一致」「力の大きさが同じ」「力の向きが互いに反対」である必要があります。
また、力の表示の仕方は、一般的に矢印で表示されます。矢印の長さが力の大きさを、矢印の向きが力の向きを、矢印の始点または終点が力の作用点を表しています。
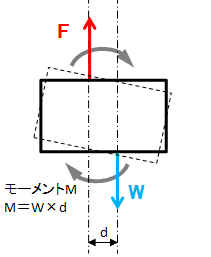
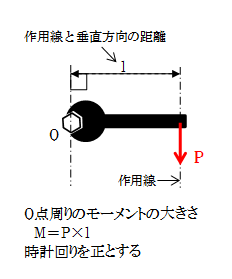
簡単に考えるために、物体(鞄)が剛体(=力を加えても変形しない物体)とすると、物体に作用する2つの力の作用線が一致していない場合、図1-1-2のように物体が回転してしまいます。この物体を回転させる力のことをモーメントMといいます。このモーメントの大きさは、力の大きさPと回転中心から力の作用点までの垂直方向の距離lを掛けた値、すなわち、M=P×l となります(図1-1-3参照)。
また、図1-1-2に示す2つの力FとWは、作用線が並行で大きさが同じ逆向きの力となります。この一対の力のことを「偶力」といいます。