今回は、力学について解説していきます。
自分なりに手書きでそれぞれの問題を解いてみました。その上で、考え方について解説していきます。
〔No.1〕

M≦Myの場合と、M=Mpの場合の断面の応力度を考えます。
まず、M≦Myの場合では、断面の縁応力度が降伏応力度に達するまでの状態(弾性)となります。この場合、図心位置=中立軸位置となります。
図のように、T型断面を2つの断面として分けて考えてそれぞれの図心位置を求めます。
また、M=Mpの場合(全塑性モーメント)では、圧縮側と引張側が全て降伏応力度σyとなる状態となります。応力として釣り合う状態とならないといけないので、
N=σy×An(An=圧縮側断面積)
T=σy×At(At=引張側断面積)
とすると、T=Nであることから、
σy×An=σy×At ⇒ An=Atとなる位置が中立軸位置となります。
〔No.2〕

ここでのポイントは、「接触面の摩擦が無い」⇒分割された断面はそれぞれの部材に力が作用するということです。
梁B及び梁Cは、分割した2つの各断面は同じ断面形状なので、1/2Pが作用します。その力が作用した場合に、分割した片方の部材のたわみを求めます。
(分割した片方の部材の断面2次モーメントを求めます。)
〔No.3〕

モーメント図を求める問題の解き方は、「変形をイメージ」することで、「曲げモーメント図」を描くことができます。
A点に10Pの力が作用する場合、B点にM=10PLの曲げモーメントが発生します。
この「M=10PL」の曲げモーメントが、右の部材と下の部材に分担されます。この分担の割合は、曲げ剛性による分担割合となります。
今回の場合では、曲げ剛性が2EIと3EIなので、
右の部材には、10PL ×(2EI/(2EI+3EI))=4PL
下の部材には、10PL ×(3EI/(2EI+3EI))=6PL
にそれぞれ曲げモーメントが分配されます。
また、端部は剛接合ですので、端部に発生する曲げモーメントは、
B点に発生する曲げモーメントとは反対側向きに1/2の大きさとなります。
〔No.4〕
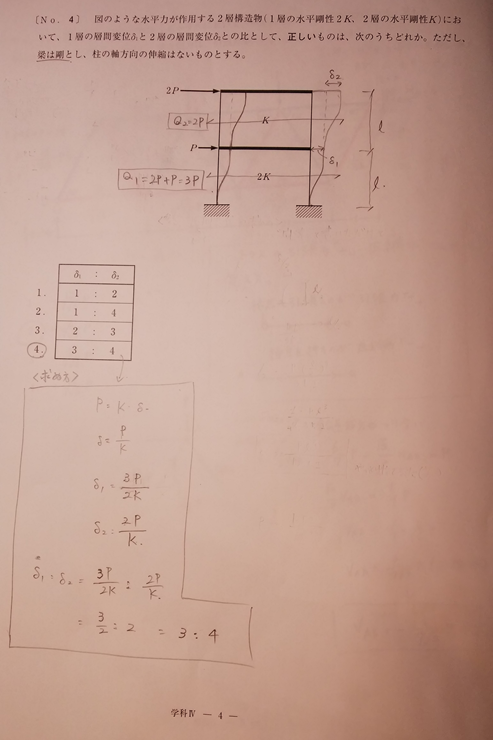
各階の層間変位δと層せん断力Q、剛性Kの関係は、
δ=Q/K
となります。
各階の層せん断力は、
Q2=2P Q1=2P+P=3P
となります。よって、各階の層間変位は、
δ2=Q2/K2=2P/K
δ1=Q1/K1=3P/2K
となります。
〔No.5〕

トラス構造の問題は、
①支点の反力を求める。
②-1 節点法:支点位置の節点の力の釣り合いから、トラス部材の軸力を求める。次に、その隣の節点の力の釣り合いから…というように求めたい部材の軸力まで計算していく。
②-2 切断法:応力を求めようとする部材のある箇所でトラスを仮に切断して、力の釣り合いより求めたい部材の軸力を算出していきます。
今回は、②-1 節点法で計算をしています。(だって、節点法の方が、各トラスの軸力の変化が分かって面白いので…)
〔No.6〕
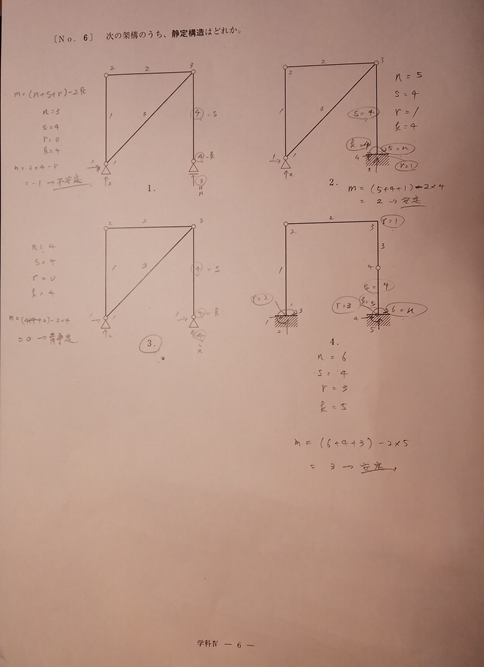
静定構造の問題は、
m=(n+s+r)-2k
n:支点反力の数(鉛直、水平、曲げ)
s:部材数
r:剛接節点数
k:節点数
の判別式により、算定してmの数値によって下記の通り判定します。
m>0:不静定構造(支点反力を1つ取り除いて(剛接合→ピン接合に変えて)も不安定にならない構造)
m=0:静定構造物(支点反力を1つ取り除く(剛接合→ピン接合に変える)と不安定になる構造)
m<0:不安定構造(力を加えると移動したり崩れてしまう構造)
計算をしています。(だって、節点法の方が、各トラスの軸力の変化が分かって面白いので…)