ここでは、力が作用している部材の断面上に生じる応力度(=単位面積当たりの応力)について解説していきます。
下図に示すように棒がで引っ張られると、棒の断面には引張力(軸方向力)が発生します。この場合、この軸方向力は棒の断面に垂直方向に、均一に発生する応力度σを足し合わせた力です。

ここで応力度σとは、「単位面積当たりの応力」で表します。棒に作用する引張力をP、棒の断面積をAとすると、
σ=P/A
の関係があります。
棒が引っ張られると、当然棒は「変形」をします。横方向への変形量をΔLとすると、棒は両側から引張力Pによって引っ張られているので、両端側がΔL/2ずつ変形をしています。

先ほどの応力度(=単位面積当たりの応力)と同様に、長さについても、ひずみε「単位長さあたりの変形量」と表します。棒の長さをLとすると、ひずみεは、
ε=ΔL/L
の関係があります。
ここまで、「応力度」と「ひずみ」について説明してきました。ここで、棒が引っ張られると変形することから、応力度σとひずみεには何かしらの関係があると考えることができます。この関係を調べるために、棒鋼の引張試験やコンクリートの圧縮試験を行ったりします。
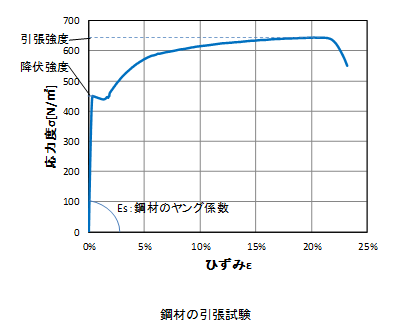

両方の図より、ひずみが小さい範囲においては応力度とひずみは「比例関係(線形領域)」にあります。この比例関係成立する範囲の材料の性質を「弾性」と呼びます。また、この直線の傾きのことを「ヤング係数:E」と呼ばれる比例定数で表します。つまり、
σ=E×ε
の関係が成り立ちます。すなわち、ヤング係数:Eとは部材の伸び縮みのしにくさ(=硬さ)を表したもので、ヤング係数が大きいと伸び縮みがしにくい(=硬い)材料であることを意味しています。
また、材料ごとのヤング係数として、
鋼材のヤング係数:Es=2.05×105
普通コンクリートのヤング係数:Ec=鋼材の約1/10程度
となります。
一方で、実際に建築物に大きな地震を受けると、建築物に使用している材料は弾性範囲(弾性域)を超えて塑性範囲(塑性域)と呼ばれる応力度とひずみが比例関係(線形領域)ではない領域(=非線形領域)に達します。
弾性範囲においては、応力が降伏点に達する前までに力を取り除くと変形が0に戻りますが、塑性範囲では荷重が増大せずに一定の値を維持しますが、ひずみが増加していきます。そして塑性範囲で力を取り除くと残留ひずみ(残留変形)が残ります。建築構造設計においては、この塑性域の状態も含めて設計する必要がありますので、とても大事な内容です。